A surprisingly new and alternative path to fault tolerant quantum computation is emerging. Fuelled by recent impressive results, “cat qubits” have been a major topic in the quantum community and have even hit the public media. At the core, cat qubits exponentially suppress bit-flip errors by an autonomous and continuous error correction mechanism.
On their superconducting chip, the French startup Alice & Bob has achieved bit-flip life-times of astonishing 10s and probably even much longer – orders of magnitudes superior to the regular superconducting qubits! In a another recent Nature publication Amazon AWS has reported about their very similar chip, that also corrects the remaining phase-flip errors, by drastically reducing the error-correction overhead compared to surface codes.
Unfortunately, it is difficult to get to the core of the new technology: Besides several high-level introductions, the details are outlined in numerous technical papers. This article is a detailed quick-guide to the fundamental concepts of the fascinating technology and related publications. It also outlines the current state of the new approach and introduces key players.
 Image by Bianca Van Dijk from Pixabay
Image by Bianca Van Dijk from Pixabay
Contents
- 1 Cat Qubits: A new path to quantum fault tolerance
- 2 Autonomous and continuous error correction
- 3 Bosonic cat states and coherent states
- 4 The birth of cat qubits
- 5 The two-photon driven, stabilizing process
- 6 Exponential bit-flip suppression
- 7 Phase-flip errors and new LDPC-codes
- 8 Implementing the two-photon driven dissipative process
- 9 The ATS-element: An important PhD-thesis
- 10 The company Alice & Bob
- 11 Amazon AWS’ quantum chip Ocelot
- 12 Bias-preserving quantum gates
- 13 Some thoughts about cat qubits
- Appendix: Adiabatic elimination of the buffer mode
- Footnotes
1 Cat Qubits: A new path to quantum fault tolerance
Nowadays, fault tolerant quantum computation seems to be omnipresent. As the current NISQ-era loses stamina, the quantum community focuses more and more on fault tolerance and early fault tolerance. Indeed, with their new superconducting chip “Willow”, the Google AI team has recently achieved a seminal milestone along this path – the break-even point of quantum error-correction. By implementing an error-correcting surface-code of code distance d=7, their logical qubit proved to be even twice as stable as all involved physical qubits!
The rest of this path is pretty much folk wisdom around the community: The industry needs to scale the chip size to about 1000 physical data qubits to implement a single logical qubit with an error rate of moderate 0,0001% (assuming a physical error rate of 0.2%) i.
By advancing the architecture to support long-range entanglement and novel quantum LDPC-codes, the physical-to-logical overhead may even be reduced by a factor 8. To execute error-codes of this size, the industry will also need to master new engineering challenges regarding syndrome measurements and classical error decoding. To support many logical qubits, a new coherent interconnection of many chips will have to be achieved as well … somehow.
Kind of surprisingly and off-the-radar of the general news coverage, a very different alternative track to fault tolerance has evolved in quantum physics in the last years. The novel approach is called “cat qubits” and by now it has become a major topic around the quantum computing folks. The development of cat qubits dates back to a very fruitful collaboration, that started around 2012 at Yale University.
The results of the team were published in two pioneering papers in 2014 and 2015. Afterwards, the two main authors of the papers returned to France and inspired even more scientists with the novel method. Among this new group were two young doctoral students, who later translated their scientific expertise into the commercial world — the founders of the French startup Alice & Bob. Starting in 2020, Alice & Bob, with currently more than 100 employees, has become a major player in the quantum world. In 2024 it published impressive results of their hardware and announced ambitious goals. In 2025 the AWS Quantum team from Pasedena published Amazon’s first quantum chip, which implements one logical cat qubit.
This article is a story about these developments. But most of all, I want to give you some deeper insights about the core concepts of cat qubits. So at first, I will outline a few technical background information for you.
2 Autonomous and continuous error correction
Stabilizing dissipative systems
Every quantum machine is subject to harmful interaction with its environment. This open, dissipative character is the reason, why the system’s state is so fragile. The corresponding density matrix dissolves into a stochastic mixture of pure states. From a physical perspective, the system produces entropy. For a quantum computer, apparently the only remedy for this problem is, to stabilize the state by executing very elaborate, discrete error correction routines on the system, such as the surface code.
But very surprisingly, there is actually an option to use dissipation to your advantage: By attaching a carefully engineered and intentionally lossy, low quality reservoir. The entropy of the system may be transferred to the subsystem composed of this ancilla reservoir and the environment, driving back the quantum system to its initial pure state.
Such a setup establishes an autonomous and continuous error correction mechanism. This kind of reservoir engineering has been studied intensively in the past couple of decades. It is the fundamental strategy behind cat qubits.
The Lindbladian equation
Keep in mind, that the dynamics of open systems is not unitary anymore and cannot be described by the Schrödinger equation. But it shows, that the time evolution of the system’s density matrix $ \rho $ (such as $ \lvert \psi \rangle \langle \psi \lvert $ for a pure state) is still strictly positive and trace preserving. It is governed by the Lindbladian equation which was formulated in the 1976s by several authors ii:
\begin{align}
\frac{d}{dt} \rho =& – \frac{i}{\hbar} [H, \rho] + \mathcal{D}[L] \rho \\
& \text{with} \\
\mathcal{D}[L] \rho :=& L \rho L^\dagger – \frac{1}{2} L^\dagger L \rho – \frac{1}{2} \rho L^\dagger L
\end{align}
Here, of course $ H $ is the usual Hamiltonian of the system and $ L $ is a “jump operator” describing the dissipative part of the dynamics. For the purpose of an dissipative error correction mechanism one aims to design a Lindbladian equation, which autonomously drives every pure or mixed density matrix to a stable set of states. Note, that here we are dealing with density matrices, so this set of states is a manifold. For the sake of implementing a logical qubit, the stable manifold should be spanned by the pure states of a well-defined code space.
During the research for this kind of reservoir engineering, bosonic quantum systems based on superconducting circuits (circuit quantum electrodynamics to be exact) proved to be an appealing platform for several reasons:
Their dominating errors are photon loss events, which reduces the complexity of the task. Also, there exists a wide variety of circuit elements. Specifically, Josephson junctions show a nonlinear character, that proves to be important for implementations. Their dispersive properties are very precise, compared to nonlinear crystals in integrated photonics for instance. Meaning: The output may be controlled very well depending on the photons’ wavelengths.
Using a single mode photonic cavity (e.g. a coplanar waveguide resonator with very little photon loss), quantum information may be encoded in so-called bosonic cat states.
3 Bosonic cat states and coherent states
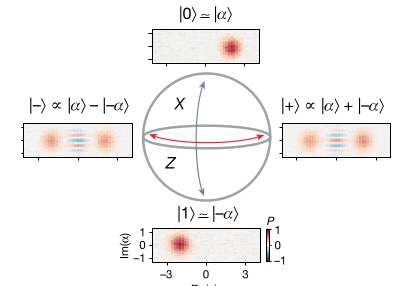
“Cat states” are named after Schrödinger’s famous thought experiment. They are a superposition of two “opposite” states with almost classical behavior. In the multi-qubit case, this is for instance a GHZ state with all-spins-up and all-spins-down.
Coherent states
In an infinite dimensional Hilbert space, like for a harmonic resonator with arbitrary numbers of photons, such a large state may be represented by a so-called “coherent state” iii:
\begin{gather}
\lvert \alpha \rangle := e^{-\frac{|\alpha|^2}{2}} \sum_{n=0}^\infty \frac{\alpha^n}{\sqrt{n!}} \lvert n \rangle
\end{gather}
Here, our Hilbert space is the Fock space with basis states representing all possible photon numbers of a single mode $(\lvert n \rangle)_n$. In our case, this mode will be the resonance frequency of the harmonic oscillator.
As usual in the Fock space notation, a photon with a fixed frequency is created by a creation operator $a^\dagger$ and destroyed by an annihilation operator $a$.
\begin{align}
a^\dagger \lvert n \rangle &= \sqrt{n+1} \lvert n+1 \rangle \\
a \lvert n+1 \rangle &= \sqrt{n+1} \lvert n \rangle
\end{align}
The states $\lvert \alpha \rangle$ show maximal coherence and an almost classical kind of behavior as a wave package. In general, their parameter $\alpha$ is complex and spans a 2d-phase space. The coherent states are complete but only almost orthogonal:
\begin{align}
\langle \beta \lvert \alpha \rangle &= e^{-\frac{1}{2}(|\beta|^2 + |\alpha|^2 – 2\beta^*\alpha)}
\end{align}
Further, the states $\lvert \alpha \rangle$ are eigenstates of the annihilation operator, because of their exponential character:
\begin{align}
a \lvert \alpha \rangle &= \alpha \lvert \alpha \rangle
\end{align}
This has interesting consequences. For instance, their expectation value for the photon number $ N = a^\dagger a $ is:
\begin{align}
\langle N \rangle = \langle \alpha \lvert a^\dagger a \lvert \alpha \rangle &= \langle a \alpha \lvert a \alpha \rangle = |\alpha|^2
\end{align}
Thus, we may interpret the complex parameter $\alpha$ as an “amplitude” of the coherent state.
Another consequence is the following: A coherent state inside a harmonic resonator is subject to single-photon loss, which is usually the dominant error channel $L=\sqrt{\kappa_1} a$. Thus, the coherent state constantly loses energy of the form
\begin{align}
\lvert \alpha(t) \rangle &= \lvert \alpha \cdot e^{- \kappa_1 t /2 } \rangle \rightarrow \lvert 0 \rangle
\end{align}
So, to stabilize a coherent state, one definitely needs a way to pump energy back into the system. On the other hand, if we turn off this pump, the state will converge to the vacuum state. This will be useful for state preparation.
Cat states
Using the coherent states, we are now ready to introduce the even and odd cat states iv:
\begin{align}
\lvert C_\alpha^\pm \rangle := N_\alpha^\pm \left( \lvert \alpha \rangle \pm \lvert -\alpha \rangle \right)
\end{align}
Using the exponential expansion of $\lvert \alpha \rangle$, we see, that $ \lvert C_\alpha^+ \rangle $ contains only an even number of photons and $ \lvert C_\alpha^- \rangle $ only an odd number of photons. The $ N_\alpha^\pm $ are constants.
For completion, we also consider an additional pair of cat states:
\begin{align}
\lvert C_{i\alpha}^\pm \rangle := N_{i\alpha}^\pm \left( \lvert i \alpha \rangle \pm \lvert – i \alpha \rangle \right)
\end{align}
As a spoiler: Of course, the even and odd cat states will be part of our stable manifold. Note, that the vacuum state $\lvert 0 \rangle$ of the resonator also has an even number of photons. If we are able to design the Lindbladian equation above in such away, that the parity number of the photons is strictly conserved, we already have a handy solution for state preparation: Just let the vacuum state evolve autonomously. Pretty nice 😉
Also, the vacuum state of the “buffer” (the reservoir) will play an important role as a solution of the 0’th perturbation order later on.
But now it’s about time to get to business.
4 The birth of cat qubits

Cat qubits were born around 2012-2014 in the lab of Michel Devoret for Applied Physics at Yale University. Two pioneering results of the group were published in 2014 and 2015.
- 1. “Dynamically protected cat-qubits: a new paradigm for universal quantum computation”, by Mazyar Mirrahimi et al, outlined the theoretical framework of the new approach in 2014 v
- 2. “Confining the state of light to a quantum manifold by engineered two-photon loss”, by Zaki Leghtas et al, demonstrated the first experimental implementation of the theory in 2015 vi vii
Born in 1981, Mirrahimi showed his scientific and mathematical talent already at a young age back in Tehran, Iran. In particular, he won the silver medal at the International Mathematical Olympiad. This achievement facilitated his move to France, where he enrolled at École Polytechnique to study physics. After defending his PhD in 2005 at Caltech, while working with Nobel laureate Serge Haroche, he decided to focus his research on feedback control. In 2011, he obtained his Research Director accreditation at Inria, one of the major scientific facilities in France.
In the same year Mirrahimi started his stay at Yale as a visiting scientist, collaborating with Michel Devoret, Robert Schoelkopf and others who also kept contributing to the research on cat qubits later on. The Yale-group was also joined by Mirrahimi’s young doctoral student Zaki Leghtas from Paris viii ix.
We may summarize the main concepts of cat qubits the following way:
- Design a dissipative system, that is able to stabilize two pure coherent states. This means: If one of those states is locally perturbed in phase space, the system will drive it back to the original state. This includes any stochastically mixed state as long as the error is local in phase space. Even superpositions will be restored, while remaining phase-error issues, to be corrected in other ways (see below).
- By separating their distance $\alpha$ in phase space, we may exponentially suppress the overlap of the two states and along any bit-flip error.
- Next, build a real system, that effectively implements the Lindbladian, that we have designed before on a theoretical level. We need to ensure, that the major error channels are local in phase space.
- Now, we have a system with a very biased noise channel: It only produces phase-flip errors. Those may be suppressed by a standard repetition code, which needs much less resources and control, than a surface code.
- At last, we need gates, that preserve this bias at the cat qubit level and also enable universal quantum computation on the logical level.
In the rest of the article, we will discuss these points in detail and relate these to recent papers.
5 The two-photon driven, stabilizing process
In the following sections I make heavy use of the great lecture notes “Quantum computation with cat qubits” from Les Houches Summer School by J. Guillaud, J. Cohen and M. Mirrahimi. It is an in-depth introduction to cat qubits x. But it is also a 75-pages long, graduate-level report. So, I advice you to keep reading this article, which summarizes important punchlines and provides additional information.
As stated above, we are looking for a dissipative process, that stabilizes two coherent states. This will implement one stabilized qubit. It is known, that a dumped quantum resonator, which is driven in resonance and dissipatively coupled to a bath, stabilizes one coherent state by a regular single-photon process. It is reasonable to ask, if this knowledge may be used in a non-standard way to stabilize two states. The clever solution for this was, to “square” the equation of the regular single-photon process, which gives an artificial two-photon driven process.
\begin{align}
\frac{d}{dt} \rho =& -i \epsilon_2 \left[e^{-i \phi_d} a^{\dagger 2} + e^{i \phi_d} a^2, \rho \right] + \kappa_2 \mathcal{D}[a^2] \rho
\end{align}
This Lindbladian describes a harmonic oscillator, in the rotating frame of the drive, with the two-photon dumping rate $\kappa_2$, the amplitude of a two-photon-drive $\epsilon_2$ and $\phi_d$ its phase shift. This may be regrouped as:
\begin{align}
\frac{d}{dt} \rho =& \kappa_2 \cdot \mathcal{D} [a^2 – \alpha^2] \rho \\
& \text{with} \\
\alpha =& e^{-i \frac{\phi_d}{2} } \sqrt{- \frac{2i \epsilon_2}{ \kappa_2}} \sim \sqrt{ \epsilon_2}
\end{align}
Any pure state with $L \lvert \psi \rangle = 0$ for the dissipation operator $ L = a^2 − \alpha^2$ is necessarily a fixed state of the dynamics with $ \frac{d}{dt} \rho = 0 $. As coherent states are eigenstates of the annihilation operator $a$, we already know that $\lvert \alpha \rangle$ and $\lvert -\alpha \rangle$ are in this kernel. Even better, the same is also true for all superpositions, as $L$ is linear
\begin{align}
\text{kernel}(L) =& \text{ span} \{\lvert \alpha \rangle, \lvert -\alpha \rangle \}
\end{align}
Now we have found our stable, pure states
\begin{align}
\lvert 0 \rangle_c :=& \lvert \alpha \rangle \\
\lvert 1 \rangle_c :=& \lvert -\alpha \rangle
\end{align}
To be exact, we have to add an exponential error-term, as the coherent states are not orthogonal $ \lvert 0 \rangle_c = \lvert \alpha \rangle + O(e^{-2|\alpha|^2}) $, $ \lvert 1 \rangle_c = \ldots$.
Note, that the following identities are exact:
\begin{align}
\lvert + \rangle_c =& \lvert C_\alpha^+ \rangle \\
\lvert – \rangle_c =& \lvert C_\alpha^- \rangle
\end{align}
By the way: in his original paper, Mirrahimi discussed the orthogonal cat states $ \lvert C_\alpha^\pm \rangle $ as logical quantum states, which resulted in an exponential phase-flip suppression.
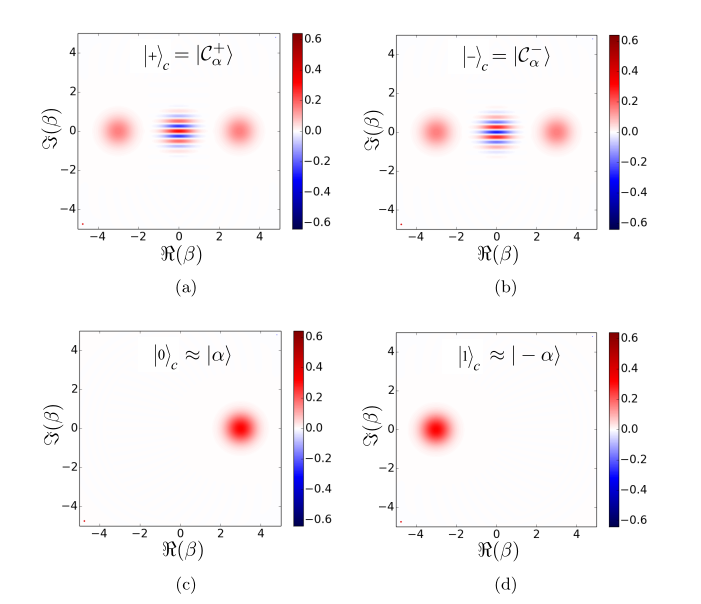
credits by Guillaud, Cohen, Mirrahimi CC BY 4.0, via scipost.org, from lecture notes “Quantum computation with cat qubits”
From this definition we already see a few important consequences:
- The overlap of the stable, logical states vanishes exponentially in the drive amplitude $\epsilon_2$. This is an indication, that we just need to increase the power of the drive a little bit to suppress the bit-flip error much further.
- But if we increase the amplitude $\alpha$, we also increase the mean photon number $\langle N \rangle \sim \epsilon_2 $. This will also increase the single-photon loss of our memory which is an undesired term, that we haven’t considered so far. Such losses will result in phase-flip errors. But we expect this effect to be only linear as explained below.
As all photon-exchanges of the oscillator with the drive and the bath occur in pairs, the parity of the system is conserved. Above, we already saw, that this will drive the vacuum state into the even cat state.
\begin{align}
\lvert 0 \rangle \rightarrow \frac{1}{\sqrt{2}} \left( \lvert \alpha \rangle + \lvert -\alpha \rangle \right)
\end{align}
It is crucial to know, what the other and possibly mixed states will be driven into. We will look into this in the next section. Before I finish this one, I want to emphasize another point from Mirrahimi’s original paper:
The concept of the two-photon-drive may be extended to the concept of a 4-photon process and even an $r$-photon process. Likewise, the results above may be generalized by replacing $ 2 \rightarrow 4 $ or $2 \rightarrow r$. A four-photon process results in a stable manifold spanned by the four coherent states $\lvert \alpha_4 \rangle, \lvert -\alpha_4 \rangle, \lvert i\alpha_4 \rangle, \lvert – i \alpha_4 \rangle $ and an adapted $\alpha_4$. The benefit of such a manifold is, that here we could define a different logical scheme, that suppresses bit- and phase-flip errors. Even though such a system may still be possible, the current implementations of cat qubits use the two-photon process which corrects only bit-flip errors.
6 Exponential bit-flip suppression
In the lecture notes from Les Houches (section 2.3) you may find a detailed discussion of the error suppression for $\rho(t)$ in our dissipative master equation. Here, it is sufficient to analyze the asymptotic dynamics of an arbitrary pure coherent state.
\begin{align}
\rho(0) =& \lvert \beta \rangle \langle \beta \lvert
\end{align}
The result of this derivation is visualized by this semi-classical vectorfield representation:
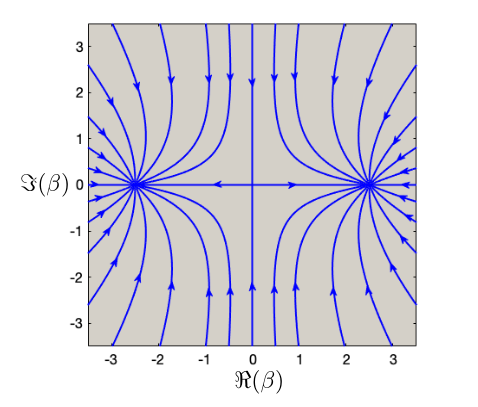
Here you may see, that the density matrix of every perturbation $\beta$ in each half plane will be driven back to a stable fix-point, the logical state in this half plane $ \lvert \alpha \rangle $ or $ \lvert -\alpha \rangle $. This happens at a rate $\kappa_\text{conf}$ with
\begin{align}
\kappa_\text{conf} = 2|\alpha|^2 \cdot \kappa_2
\end{align}
The rate induces an operation time of the stabilizing process of $ T= \kappa_\text{conf}^{-1} $.
Only the very narrow strip in the center will be driven to an instable saddle point, the superposition $ \lvert + \rangle_c $.
The analysis shows, that the larger $\alpha$ is chosen, the more does the system behave as visualized by this ideal picture.
Note, that even locally perturbed mixed states may be corrected to pure states:
\begin{align}
\rho(0) =& (1-p) \cdot \lvert \alpha \rangle \langle \alpha \lvert + p \cdot \lvert \alpha + \epsilon \rangle \langle \alpha + \epsilon \lvert
\end{align}
As the Lindbladian is a linear equation, this mixed state will be driven to
\begin{align}
\rho(t) \rightarrow & (1-p) \cdot \lvert \alpha \rangle \langle \alpha \lvert + p \cdot \lvert \alpha \rangle \langle \alpha \lvert = \lvert \alpha \rangle \langle \alpha \lvert
\end{align}
Thus, the two-photon process is able to drive entropy out of the system as hinted in the introduction above.
Also, superpositions of locally perturbed states will be corrected to superpositions in the stable manifold.
The authors of the lecture notes outline, that dominant error channels indeed transform $ \lvert \alpha \rangle $ to nearby coherent states $ \lvert \beta \rangle $. These will be corrected by the two-photon process, such as
- Single-photon loss $ \kappa_1 \cdot \mathcal{D}[a] $
- Markovian photon dephasing $ \kappa_\Phi \cdot \mathcal{D}[a^\dagger a] $
We already got an impression of the local character of a single-photon loss channel above (without the two-photon process turned on).
The numerical simulation of the complete Linbladian gives the following diagram:

7 Phase-flip errors and new LDPC-codes
The coherent states will be restored after a single-photon loss or after thermal energy damping. But this does not correct a phase change, that the error possibly caused in a superposition. In particular, a single-photon loss would transform an even cat state into an odd cat state with reduced amplitude. This will be “corrected” to an the odd cat state in the stable manifold:
\begin{align}
\lvert + \rangle_c = \lvert C_\alpha^+ \rangle \rightarrow \lvert C_\beta^- \rangle \rightarrow \lvert C_\alpha^- \rangle = \lvert – \rangle_c
\end{align}
Likewise a thermal energy dumping will transform a superposition of the form $\lvert + \rangle_c$ to a statistical mixture of $\lvert + \rangle_c $ and $ \lvert – \rangle_c $, while the two-photon process is active.
Mazyar Mirrahimi argues in his talk for the Qiskit Seminar, that the qualitative behavior of the bit-flip and phase-flip error-rates is similar as in the standard 1d-repetition code xi:
\begin{align}
\lvert 0 \rangle_R =& \lvert 0 \dots 0 \rangle = \lvert 0 \rangle^{\otimes d} \\
\lvert 1 \rangle_R =& \lvert 1 \dots 1 \rangle = \lvert 1 \rangle^{\otimes d} \\
\end{align}
Here, a logical error occurs, if
- logical bit-flip error: most of the $d$ qubits flipped (rate $\kappa \sim e^{-d \ldots} $)
- logical phase-flip error: any of the $d$ qubits phase-flipped (rate $\kappa \sim d $)
In the case for cat qubits, this behavior was confirmed by experiments xii.
To reduce phase-flip errors, our resonator needs to be of a high-quality regarding single-photon losses. In contrast the two-photon dumping rate $\kappa_2$ should be rather lossy, as this also increases $\alpha$.
Mirrahimi outlines in his talk, that phase errors may be corrected up to $10^{-10}$ with a standard 1d-repetition code. Even better: Alice & Bob recently published a new strategy in Nature magazine, based on 2d-LDPC codes, which are even local. This new scheme significantly outperforms the 1d-repetition-code without sacrificing locality. This is in contrast to other LDPC-codes which need long-range entanglement. Also, a universal logical gate set may be realized xiii.
To be exact, Alice & Bob estimates, that a 2d-chip with 758 cat qubits could realizes 100 logical qubits with an error rate of $10^{-8}$. This might even make a single 100 logical-qubit chip within reach, without the need to interconnect several superconducting quantum chips.
8 Implementing the two-photon driven dissipative process
So far, our two-photon process is only a theoretically model. How can we actually implement it? Mirrahimi’s idea was to introduce an additional lossy buffer-system $b$, that mediates the two-photon exchange of the high-quality memory-system $a$ with the environment and with the drive:
\begin{align}
\frac{H_2}{\hbar} =& g_2 \cdot a^2 b^\dagger + g_2^* \cdot a^{2 \dagger} b
\end{align}
Here, the memory couples non-linearly to the buffer with coupling strength $g_2$. We will see below, how this may be designed in a superconducting circuit. The buffer exchanges photons with the environment and with the drive in singles:
\begin{align}
\frac{d}{dt} \rho =& -i \left[g_2 \cdot a^2 b^\dagger + g_2^* \cdot a^{2 \dagger} b, \rho \right] – \left[\epsilon_d \cdot b^\dagger + \epsilon_d^* \cdot b, \rho \right] + \kappa_b \mathcal{D}[b] \rho
\end{align}
Here, the complex $\epsilon_d$ is the amplitude and phase of the drive. This may be rearranged to
\begin{align}
\frac{d}{dt} \rho =& -i \left[g_2 \cdot \left( a^2 – \alpha^2 \right) b^\dagger + g_2^* \cdot \left( a^{2 \dagger} – \alpha^2 \right) b, \rho \right] + \kappa_b \mathcal{D}[b] \rho \\
& \text{with} \\
\alpha =& \sqrt{- \frac{\epsilon_d}{g_2}}
\end{align}
The complete system may be schematically visualized by the following setup:
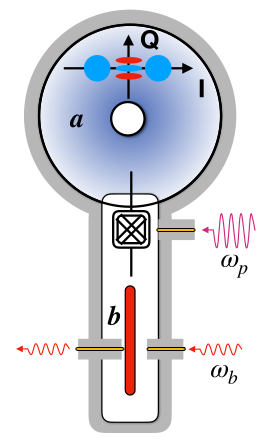
The 3d-cavity is the high-quality memory $a$ with the stabilized cat states $Q$. The red strip-line is the lossy buffer, that is resonantly driven with frequency $\omega_b$ and loses photons through the port on the left. Additionally, a pump drives the buffer with a carefully chosen frequency $\omega_p$. We will see below, how this frequency is selected. Not shown is the resonance frequency $\omega_a$ of the memory.
Before we get into a real chip, we would like to know, the answer to a crucial question: Is such a system really equivalent to the theoretical two-photon process?
Of course, the answer is “yes”. One may derive an effective equation without the buffer, by tracing out system $b$. This gives the reduced density matrix of the memory-subsystem:
\begin{align}
\rho_s =& \text{tr}_b(\rho)
\end{align}
The technique for this, is called “adiabatic elimination” and I outline it in the appendix “Adiabatic elimination of the buffer mode”.
Another core concept of cat qubits is the realization of the non-linear circuit element, that couples the memory with the buffer:
9 The ATS-element: An important PhD-thesis
In its first implementation Leghtas et al used a single Josephson junction with two antennas coupling the memory with the buffer. But this element introduced additional parasitic side effects. After his post-doctoral research at Yale, Zaki Leghtas returned to France in 2015 and obtained a professorship at Mines Paris. There, he also joined Mirrahimi at the QUANTIC team, a collaboration of Inria Paris, Mines Paris – PSL, École Normale Supérieure (ENS), CNRS and Sorbonne Université. Closely connected to the QUANTIC team is also the Quantum Circuit Group of ENS Lyon.
In 2019 Leghtas’ doctoral student Raphaël Lescanne made a significant advance in his PhD-thesis for the non-linear circuit-element. The experiment was the first implementation of a cat qubit, that achieved a bit-flip error suppression below threshold. The bit-flip lifetime of the cat qubit was 1 millisecond, a 300-fold improvement over the resonator intrinsic lifetime. The research was published in Nature in 2020 xiv.
With the help of Théau Peronnin, a PhD-candidate from ENS Lyon and Peronnin’s supervisor Benjamin Huard, Lescanne introduced a new element called Asymmetrically Threaded SQUID (ATS), which is by now a standard element of the setup. An ATS consists of a SQUID (a Superconducting Quantum Interference Device) shunted in its center by a large inductance, thus forming two loops. In the experiment, the inductance was built from an array of 5 Josephson junctions.
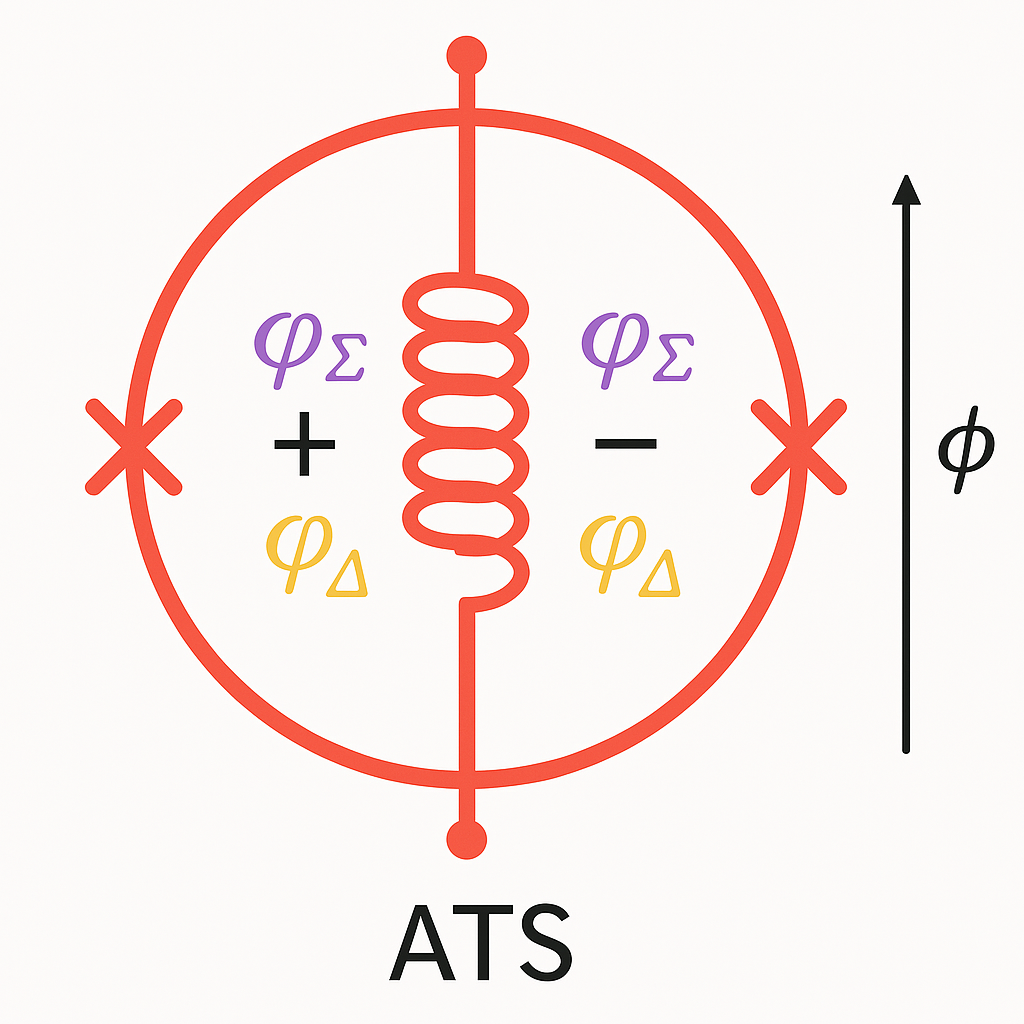
This ATS produces a complex potential $ U(\varphi)$.
\begin{align}
U(\varphi) = -2E_J \cdot cos(\varphi_\Sigma) \cdot cos(\varphi + \varphi_\Delta) + \frac{1}{2}E_L \varphi^2
\end{align}
This potential significantly simplifies at the point $\varphi_\Sigma = \varphi_\Delta = \pi/2$, which threads the left and right loops with flux $\pi$ and $ 0 $.
\begin{align}
\varphi_\Sigma =& \frac{\pi}{2} + p(t) \\
\varphi_\Delta =& \frac{\pi}{2}
\end{align}
A Taylor-expansion to 3rd order gives:
\begin{align}
U_3(\varphi) \sim & p(t) \varphi^3
\end{align}
Now one considers the global phase across the ATS dipole in Fock-space notation:
\begin{align}
\varphi = & \varphi_a \cdot \left( a + a^\dagger \right) + \varphi_b \cdot \left( b + b^\dagger \right)
\end{align}
In the complete Hamiltonian
\begin{align}
H / \hbar =& \omega_a a^\dagger a + \omega_b b^\dagger b + U_3 + \left( \epsilon_d e^{-i\omega_d t} + \epsilon_d^* e^{i\omega_d t} \right) \left( b + b^\dagger \right)
\end{align}
one obtains the desired interaction term under the condition:
\begin{align}
\omega_p = & 2 \omega_a – \omega_b \\
\frac{H_2}{\hbar} =& g_2 \cdot a^2 b^\dagger + g_2^* \cdot a^{2 \dagger} b
\end{align}
10 The company Alice & Bob
In 2020, the two doctoral colleagues Raphaël Lescanne and Théau Peronnin founded the French startup Alice & Bob. Since then, it has managed to attract key researchers of the field. Currently Alice & Bob employs more than 100 employees of several nationalities and has lately successfully raised €100 million in a series B funding round. Among its scientific advisors are Mirrahimi, Leghtas and Huard. The companies headquarter is located in Paris and by now an additional office in Boston, MA has been opened. Luckily, for the sake of this article, the startup is very active in “teleporting” the technology to the community.
In 2024 Alice & Bob et al published another significant improvement of their setup in Nature magazine xvi.
In previous experiments, the quantum tomography of the memory was performed via an ancillary system composed of a standard transmon and its readout resonator. This introduced additional error sources. In their 2024-paper, the team introduced a so-called holonomic gate to probe the quantum state. The holonomic gate does not require any additional elements but re-uses the existing memory, the buffer and the drive with an additional operational protocol. In this setup Alice & Bob achieved a macroscopic bit-flip lifetime of 10 seconds, while maintaining phase-flip times above 490 nanoseconds.
At Q2B Silicon Valley December 2024, Alice & Bob announced an even newer publication in progress, with bit-flip lifetime of 430 seconds xvii. They also work on a 8 cat qubit chip, to implement a repetition code and correct phase-flip errors.
This milestone was already officially achieved by the AWS quantum team in February 2025.
11 Amazon AWS’ quantum chip Ocelot
In yet another Nature publication, Amazon’s AWS quantum team (at Pasadena, CA, USA) describes a new quantum chip containing 5 cat qubits. Along the bit-flip suppression, the new chip successfully implements the repetition code to correct phase-flip errors xviii.
Their data qubits work similar to the ones used by Alice & Bob. Namely, each high-quality coplanar waveguide resonator (blue) is coupled by an ATS to a low-quality-buffer (green), damped through a multi-pole filter. The repetition code requires syndrom measurements on ancilla qubits (orange) which couple two adjacent cat qubits via CNOT-operations. The AWS quantum team uses standard transmon qubits as ancillas. These couple neighboring memory modes by tunable couplers.
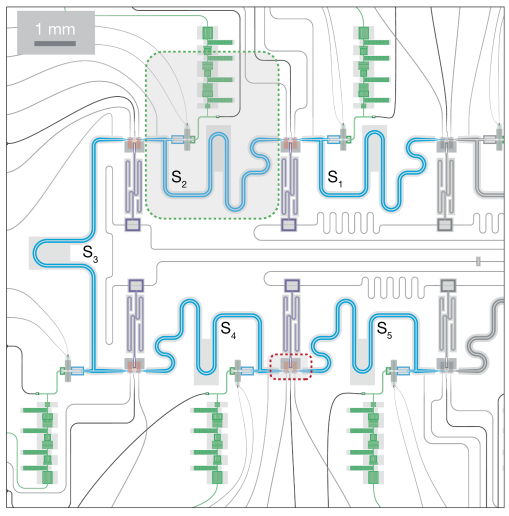
credits by AWS Center for Quantum Computing, CC BY 4.0, via Nature Open access
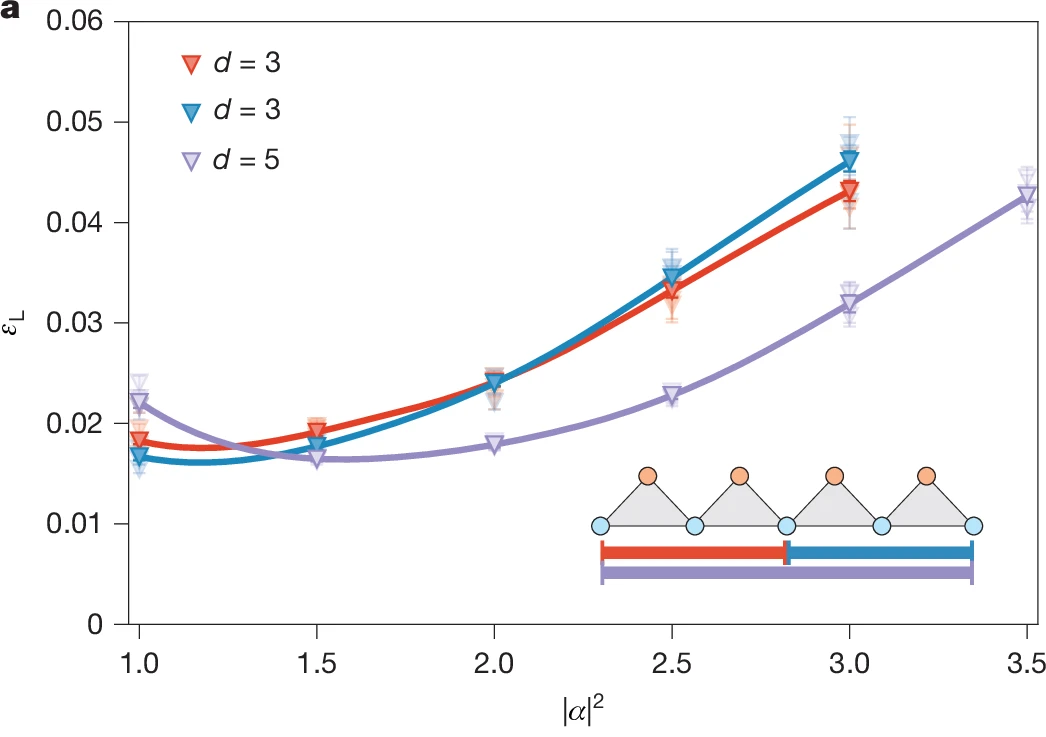
As expected, the additional circuit elements reduce the performance of the bit-flip protection. Remarkably, the AWS team manages to reach a bit-flip lifetime of 1 ms, using a relatively small mean photon number of $ |\alpha|^2 = 2 $. In this regime the phase-flip protection reaches lifetimes of 27–33 μs. As a comparison: Alice & Bob used a mean photon number up to $ |\alpha|^2 =11.3 $ in their $10s$-experiment.
The authors compare the overall logical error-rate $\epsilon_L$ (bit-flip plus phase-flip) for distance-3 and distance-5 repetition codes. They demonstrate, that the distance-5 code outperforms the distance-3 codes for different mean photon-numbers $|\alpha|^2$. This indicates, that their quantum chip even operates below threshold.
A crucial part of Amazon’s experiment was the implementation of the CNOT-gate, which successfully enabled the repetition code. In general, quantum gates for cat qubits are a tricky subject and impose constraints, that are not present in architectures using standard transmon qubits.
12 Bias-preserving quantum gates
To complete this introduction to cat qubits, we have to take a closer look at quantum gates. Since our qubits are noise-biased, this imposes challenges on the type of quantum operations, that are allowed for the qubits:
This is easily illustrated using a Hadamard gate $H$. The Hadamard transforms the computational basis $ \lvert 0 \rangle $, $ \lvert 1 \rangle $ into the states $ \lvert + \rangle $, $ \lvert – \rangle $ and vice versa. Thus, a phase-flip error $Z$ happening just before the Hadamard, will be transformed to a bit-flip error $X$. In other words:
\begin{align}
H \cdot Z = X \cdot H
\end{align}
This would destroy our noise-bias. What we need to have, are bias-preserving gates. This induces a constraint of the type of operations, that are allowed. As we just saw: A Hadamard gate is not allowed. This is a problem for universal quantum computation at the cat qubit level. Below, we will see, how this is solved at the logical level.
Additionally, as a second requirement, the generally allowed operations will have to be implemented in a bias-preserving manner.
The argument may be generalized: We need operations $U$, that commute with $Z$ or at least, do not translate $Z$-type errors into $X$-type or $Y$-type errors. For instance, $Z(\varphi)$ is obviously bias-preserving. $X=X(\pi)$ and $Y(\pi)$ are bias-preserving, because of their anti-commutation rules, e.g. $\{X, Z\}=0$. The same holds for a CZ- and a CNOT-gate. In general, we need:
\begin{align}
U \cdot Z =& Z \cdot \left(a I – ib X – ic Y \right) \cdot U \\
& \text{with} \\
b =& c = 0
\end{align}
In the lecture notes from Les Houche, the authors parameterize $U, a, b, c$ by a general rotation in the Bloch sphere $ U = \mathcal{R}_\vec{n}(\varphi)$ and derive the constraints for the parameters $n_x, n_y, n_z, \varphi$. A similar analysis, may be carried out for two-qubit gates.
But, one also has to keep the second requirement in mind. Although an $X$ gate is bias-preserving in general, it is actually impossible to implement it in a bias-preserving manner — without leaving the code space. This may be visualized by a gradual $\pi$-rotation of $\lvert 1 \rangle$ around the $X$-axis in the Bloch sphere: A $Z$-error happening in the middle of the operation on the intermediate state $ \lvert + \rangle$, will return the Bloch vector to its original position after the full X-rotation is completed: a bit-flip error.
Implementations of X, CX, SWAP, CCX
It is still possible to implement X-type operations by adiabatically changing the code space.
\begin{align}
\text{span} \{ \lvert \alpha(t) \rangle, \lvert -\alpha(t) \rangle \}
\end{align}
Here, adiabatically means, that the execution time $T$ of the gate is long compared to the confining time of the two-photon-stabilization $\kappa_{\text{conf}}^{-1}$. In this case, superpositions in the code-space are preserved and only their coherent states change, if both states remain well separated during the execution:
\begin{align}
\lvert \psi(t) \rangle = & c_0 \cdot \lvert \alpha(t) \rangle + c_1 \lvert -\alpha(t) \rangle
\end{align}
An $X$ gate is implemented by choosing a path, that exchanges $\lvert \alpha \rangle $ and $\lvert -\alpha \rangle $, e.g
\begin{align}
\alpha(t) = \alpha \cdot e^{i\pi \cdot t/T}
\end{align}
Note, that for a two-qubit gate, one needs to choose two different paths $\alpha_2(t)$ for the target memory 2, depending on the state of the control memory 1. This may be done, by coupling a single buffer to two high-quality resonators. In the case of a CNOT, this is visualized by the following image:
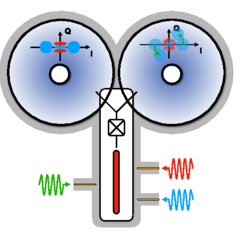
Implementations of Z(θ), ZZ(θ), ZZZ(θ)
Z-type gates may be implemented by the quantum Zeno effect, a weak resonant drive of the memory with a Hamiltonian $H_Z$ establishes the dynamical phase in the code space. E.g.
\begin{align}
H_Z = \epsilon_Z a + \epsilon_Z^* a^\dagger
\end{align}
Likewise for an entangling gate on two memories:
\begin{align}
H_{Z_1 Z_2} = \epsilon_{Z_1 Z_2} \cdot a_1 a_2^\dagger + \epsilon_{Z_1 Z_2}^* \cdot a_1^\dagger a_2
\end{align}
Logical gates and universal gate set
We have to keep in mind, that cat qubits are not the end of the game. In order to establish fault tolerance, we have to include the error correction for phase-flips. A paper by J. Guillaud and M. Mirrahim from 2019 discusses a logical gate set for the case of the simple repetition code, including state preparation of $\lvert \pm \rangle$-states and X-measurements xix.
This is summarized by the following diagram:
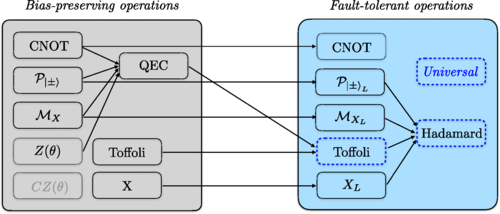
In particular, the paper illustrates, how to create a logical Hadamard gate by combining other logical operations, thus establishing universal quantum computation. Also, the authors outline, that all basic logical operations are transversal, except of the Toffoli gate. Thus, e.g. a logical CNOT is implemented by just executing the bias-preserving CNOTs on each physical cat qubit. Another very remarkable aspect is, that the proposed Toffoli gate does not require the use of costly magic states, as the 2d-surface code does.
13 Some thoughts about cat qubits
I think, the concept of an autonomous and continuous error correction is just thrilling. The exponential bit-flip error suppression seems like “halfway to a topological qubit”. Regarding the fact, that cat qubits are already there and working, I wonder, why they don’t get all the media attention.
And cat qubits are working very well. The two-photon process is a powerful tool. Take Amazon’s Ocelot-chip for instance: The CNOT-gate needs to rotate the target-qubit freely in phase space. Thus, they have to turn off the two-photon process during gate execution. The AWS team demonstrated, that this degrades the state and after subsequent CNOT-executions, the state fidelity gets bad. But these problems resolve immediately once the two-photon process is turned back on.
Pretty nice 😉
But cat qubits are also a young technology. Especially the implementation of quantum gates are at a very early stage. Furthermore, for useful computation, the exponential bit-flip suppression will have to be extended from seconds to hours. We will see, how well the approximations for the stabilizing process and the ATS will work in this regime. For instance, increasing the driving pump, will heat up the system and cause undesired side effects. Also, the overall native coherence time has to stay long enough to enable algorithmic correction of the phase-flip errors.
Personally, I am excited to see how the new technology evolves and what surprises might arise in the new setting. For instance, in the case of the logical Toffoli-gate we saw, that costly magic states may be avoided in the mentioned proposal. I wonder, what the execution time of a logical Toffoli-gate will be in the cat qubit scheme. This is a major bottleneck for fault tolerance based on surface codes (see my article “Does Quadratic Quantum Speedup have a problem?”).
These are interesting times indeed 🙂
Appendix: Adiabatic elimination of the buffer mode
As described in the main text, we would like to know the answer to a crucial question: Is the compound system, the memory and the buffer, really equivalent to the theoretical two-photon process?
To show this, one may derive an *effective/* equation without the buffer, by tracing out the modes of $b$. This gives the reduced density matrix of the memory-subsystem:
\begin{align}
\rho_s =& \text{tr}_b(\rho)
\end{align}
The technique for this, is called “adiabatic elimination” and is very nicely explained in the supplementary text of Zaki Leghtas’ paper from 2015 xx:
The compound density matrix may by expanded as a perturbation around an exact solution of zero’th order. In this case, this is the uncoupled system of the memory and the buffer. The asymptotic density matrix of the uncoupled buffer relaxes to the vacuum state. Thus, we have
\begin{align}
\rho = & \quad \quad \rho_{a, 00} \cdot \lvert 0 \rangle \langle 0 \lvert_b \\
& + \delta \cdot \left(
\rho_{a, 01} \lvert 0 \rangle \langle 1 \lvert_b
+ \rho_{a, 10} \lvert 1 \rangle \langle 0 \lvert_b
\right) \\
& + \delta^2 \cdot \left(
\rho_{a, 11} \cdot \lvert 1 \rangle \langle 1 \lvert_b
+ \rho_{a, 02} \lvert 0 \rangle \langle 2 \lvert_b
+ \rho_{a, 20} \lvert 1 \rangle \langle 0 \lvert_b
\right) \\
& + O \left(\delta^3 \right)
\end{align}
Note the generic expression:
\begin{align}
\rho_s =& \rho_{a, 00} + \delta^2 \cdot \rho_{a, 11}
\end{align}
We may derive the dynamics of $ \rho_s $, by multiplying the Lindladian master equation for $\rho$ by
- 1. $ \lvert 0 \rangle_b $ and $ \langle 0 \lvert_b $
- 2. $ \lvert 1 \rangle_b $ and $ \langle 1 \lvert_b $
As the exact analysis shows: This will give concrete relations for the dynamics of $ \rho_s$ in terms of the $\rho_{a, ij}$: The two-photon process, with an effective an effective dumping rate.
Footnotes
i https://quantumcomputing.stackexchange.com/questions/23650/how-to-calculate-the-number-of-qubits-in-surface-code-for-given-physical-error: Craig Gidney’s answer on Stackexchange
ii https://en.wikipedia.org/wiki/Lindbladian: Wikipedia-article about the Lindblad-equation
iii https://en.wikipedia.org/wiki/Coherent_state: Wikipedia-article about coherent states
iv https://en.wikipedia.org/wiki/Cat_state: Wikipedia-article about cat states
v https://iopscience.iop.org/article/10.1088/1367-2630/16/4/045014: “Dynamically protected cat-qubits: a new paradigm for universal quantum computation”, by Mazyar Mirrahimi et al, New Journal of Physics (2014 31 pages)
vi https://arxiv.org/abs/1412.4633: “Confining the state of light to a quantum manifold by engineered two-photon loss”, by Zaki Leghtas et al (Science 2015, 29 pages)
vii https://news.yale.edu/2015/02/25/yale-physicists-find-new-form-quantum-friction: “Yale physicists find a new form of quantum friction”, Yale-article about Zaki Leghtas’ work
viii https://www.inria.fr/en/mazyar-mirrahimi-inria-french-academie-des-sciences-young-researcher-award: “Mazyar Mirrahimi : Inria – French Académie des sciences Young Researcher Award”, Inria-article, introducing Mazyar Mirrahimi his work and vitae
ix https://cas.minesparis.psl.eu/~leghtas/: Zaki Leghtas’ CV at Mines Paris
x https://scipost.org/SciPostPhysLectNotes.72, https://arxiv.org/abs/2203.03222:“Quantum computation with cat qubits”, Lecture notes Les Houches Summer School, by Jérémie Guillaud and Joachim Cohen (Alice & Bob), Mazyar Mirrahimi (2022 75 pages)
xi https://www.youtube.com/watch?v=rHtdukHARO0&t=2291s: “Qiskit Seminar”-series, talk by Mazyar Mirrahimi (2022, 1:25h)
xii https://arxiv.org/abs/1907.11729: “Exponential suppression of bit-flips in a qubit encoded in an oscillator”, by Raphaël Lescanne et al (Nature 2020, 18 pages)
xiii https://www.nature.com/articles/s41467-025-56298-8: “LDPC-cat codes for low-overhead quantum computing in 2D”, by Diego Ruiz, Jérémie Guillaud et al (Nature 2025).
xiv https://arxiv.org/abs/1907.11729: “Exponential suppression of bit-flips in a qubit encoded in an oscillator”, by Raphaël Lescanne et al (Nature 2020, 18 pages)
xv https://www.youtube.com/watch?v=4Tu9lDiM5hc: “Towards Quantum Computing with stabilized cat states”, Quanta Seminar on Youtube, by Jean-Loup Ville (Alice & Bob, 2023 58 min)
xvi https://arxiv.org/abs/2307.06617: “Quantum control of a cat-qubit with bit-flip times exceeding ten seconds”, by Alice & Bob, ENS, Sorbonne Paris, ENS Lyon (2023 21 pages)
xvii https://www.youtube.com/watch?v=5LuKEUIU4ak&list=PLPm2YfzOw_RQ7s9rnpaJWj7-MznOyEo6A: “Q2B24 Silicon Valley | Jeremy Stevens, Technology Development Lead”, Alice & Bob (2024 18 min)
xviii https://www.nature.com/articles/s41586-025-08642-7: “Hardware-efficient quantum error correction via concatenated bosonic qubits”, by Harald Putterman et al, Amazon AWS, Nature (Feb. 2025 7 pages)
xix https://journals.aps.org/prx/abstract/10.1103/PhysRevX.9.041053: “Repetition Cat Qubits for Fault-Tolerant Quantum Computation”, by J. Guillaud and M. Mirrahimi (Phys. Rev. X 2019)
xx https://arxiv.org/abs/1412.4633: “Confining the state of light to a quantum manifold by engineered two-photon loss”, by Zaki Leghtas et al (Science 2015, 29 pages)